Seminar: Methoden der Nicht-differenzierbaren Optimierung
Sommersemester 2009
LV-Nr.: 0230 L 350
Seminar: Methoden der Nicht-differenzierbaren Optimierung |
||
|
|
Sommersemester 2009LV-Nr.: 0230 L 350 |
|
|
|
Prof. Dr. Dr. h.c. mult. Martin Grötschel Dr. Ralf Borndörfer Markus Reuther |
|
Das Blockseminar wird am 06. Juni 2009
im Seminarraum 2006 am Konrad-Zuse-Zentrum
für Informationstechnik
![]() auf dem Campus der Freien Universität in Dahlem (Lageplan
auf dem Campus der Freien Universität in Dahlem (Lageplan
![]() )
wie folgt durchgeführt:
)
wie folgt durchgeführt:
|
Zeit |
Thema |
Vortragender |
|
09:00 – 09:30 |
Das Bündelverfahren und seine Anwendung in NetLine |
Ivo Nowak (Lufthansa Systems GmbH) |
|
09:30 – 10:00 |
Anwendung der Bündelmethode für Integrierte Umlauf- und Dienstoptimierung im ÖPNV |
Steffen Weider (ZIB) |
|
10:00 – 11:00 |
Lagrange Relaxierung (Thema 12) |
Daniel Uwazie |
|
11:00 – 12 :00 |
Subgradientenverfahren (Thema 15) |
Marco Sarich |
|
13:00 – 14 :00 |
Konvergenz des Inkrementellen Subgradientenverfahrens (Thema 8) |
Christian Kestin |
|
14:00 – 15 :00 |
Quadratische Optimierung (Thema 9) |
Benjamin Krämer |
|
15:00 – 16 :00 |
Semidefinite Programmierung (Thema 3) |
Wei Huang |
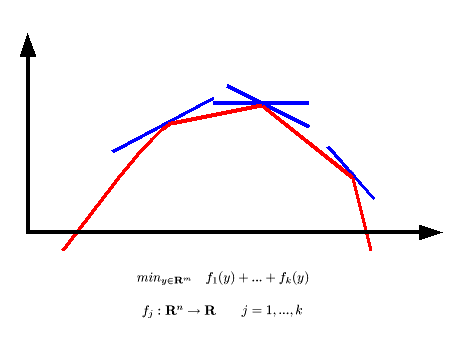
In diesem Seminar werden ausgewählte Artikel der Nicht-differenzierbaren Optimierung behandelt. Ein wesentlicher Schwerpunkt ist dabei die Bündel-Methode zur Optimierung einer konvexen Funktion. Dieses Verfahren wird z.B. in vielen kommerziellen Optimierungscodes äußerst erfolgreich für die Lösung von Relaxierungen von ganzzahligen Programmen sehr großer Dimension eingesetzt. Es sollen dabei neben den theoretischen Ergebnissen auch die praktischen Gesichtspunkte der Verfahren vorgestellt werden.
Grundkenntnisse der Linearen Algebra, Analysis sowie Kenntnisse in linearer und ganzzahliger Optimierung.
Richtlinien für die Vortragsgestaltung und die Scheinvergabe:
Die wesentliche Leistung ist ein Vortrag von ca. 50 Minuten über das zugeteilte Thema. Im Vortrag sollen in verständlicher Form wichtige Ergebnisse des (für den Vortrag zentralen) Artikels vorgestellt werden. Definitionen wichtiger Begriffe sollen stimmig vorgetragen werden. Ausgewählte Beweise sollen vorgeführt werden. Der Vortrag soll eine ansprechende äußere Form haben. Brechen Sie z.B. keine Texte zwischen Folien, wenn es sich nicht unbedingt vermeiden läßt.
Die Vortragsform und -medien kann jeder frei wählen. Als Vortragsmedien stehen Tafel, Overhead-Projektor und Beamer zur Verfügung. Insbesondere bei Beamerbenutzung sollte die Technik vorher geprüft werden.
Zum Vortragstermin ist von den Vortragenden eine etwa 5-seitige Ausarbeitung zum Thema vorzulegen. Diese wird vom Seminarteilnehmer selbst vervielfältigt und an alle Seminarteilnehmerinnen und Seminarteilnehmer verteilt. In dieser Ausarbeitung sollen wesentliche Definitionen und Ergebnisse zusammengefasst werden. Die Ausarbeitung soll in ``Publikationsqualität'' vorliegen. Dazu gehört insbesondere am Anfang ein Kopf mit Angabe von Titel, Autor, Veranstaltung und wesentlichen Quellen und am Ende ein Quellen- und Literaturverzeichnis (das im Umfang von 5 Seiten eingeschlossen ist). Es wird empfohlen, die Ausarbeitung mit Hilfe von LaTeX zu schreiben. Für LaTeX-Unkundige ist dies vielleicht ein guter Zeitpunkt, sich LaTeX anzueignen, da man im mathematischen Leben kaum darum herumkommt. (Empfehlenswerte Literatur für Einsteiger ist der erste Band der LaTeX-Serie von Helmut Kopka, erschienen bei Addison-Wesley. Bitte achten Sie darauf, dass es sich um eine ``aktuelle'' Version handelt, die LaTeX2e behandelt.)
Der Zeitbedarf für die Bearbeitung des Seminarthemas sollte nicht unterschätzt werden. Mindestens sollten insgesamt 3 Wochen, davon eine zum Lesen incl. Verstehen der Literatur, eine für den Vortrag und eine für die Ausarbeitung veranschlagt werden.
Bei der Literatursuche sind folgende Links nützlich:
Mathematische Artikel:
Zentralblatt
![]()
Mathematische Webseiten:
MathSearch
![]()
Mathematische und
Informatik-Abstracts/Bibliographie: CiteSeer
![]()
Informatikartikel/Bibliographie:
ACM Portal
![]()
Wissenschaftliches Googlen: GoogleScholar
![]()
Die Vorbesprechung mit der Themenvergabe findet statt am
Dienstag, dem 28. April 2009, um 14:00 Uhr im Raum MA315 (MATHEON-Lounge) im Mathematikgebäude der Technischen Universität Berlin, Fakultät für Mathematik.
Ein Termin mit Probekurzvorträgen von jeweils 5 Minuten Dauer
Dienstag, dem 26. Mai 2009, um 14:00 Uhr im Raum MA315 (MATHEON-Lounge) im Mathematikgebäude der Technischen Universität Berlin, Fakultät für Mathematik.
Das Seminar wird durchgeführt als Blockseminar an dem
Wochenende 6. und 7. Juni 2009 im Seminarraum 2006 am
Konrad-Zuse-Zentrum für
Informationstechnik
![]() auf dem Campus der Freien Universität in Dahlem (Lageplan
auf dem Campus der Freien Universität in Dahlem (Lageplan
![]() ).
).
Die Vorträge und Ausarbeitungen sind bis Mittwoch, den 03.06.2009 als PowerPoint- und/oder PDF-Datei bei Markus Reuther einzureichen.
|
L. Bahiense, N. Maculan, and C. Sagastizábal. The volume algorithm revisited: relation with bundle methods. 2002. [ bib ] |
|
|
A. Belloni and C. Sagastizábal. Dynamic Bundle Methods: Application to Combinatorial Optimization. [ bib ] |
|
|
C. Helmberg. Semidefinite programming. Eur. J. Oper. Res., 137(3):461-482, 2002. [ bib | DOI ] |
|
|
C. Helmberg and F. Rendl. A spectral bundle method for semidefinite programming. SIAM J. Optim., 10(3):673-696, 2000. [ bib | DOI ] |
|
|
K.C. Kiwiel. Efficiency of proximal bundle methods. J. Optimization Theory Appl., 104(3):589-603, 2000. [ bib | DOI ] |
|
|
Claude Lemaréchal, François Oustry, and Claudia Sagastizábal. The U-Lagrangian of a convex function. Trans. Am. Math. Soc., 352(2):711-729, 2000. [ bib | DOI ] |
|
|
Claude Lemaréchal and Claudia Sagastizábal. An approach to variable metric bundle methods. Henry, Jacques (ed.) et al., System modelling and optimization. Proceedings of the 16th IFIP-TC7 conference, Compiègne, France, July 5-9, 1993. London: Springer-Verlag. Lect. Notes Control Inf. Sci. 197, 144-162 (1994)., 1994. [ bib ] |
|
|
Angelia Nedić and Dimitri Bertsekas. Convergence rate of incremental subgradient algorithms. Uryasev, Stanislav (ed.) et al., Stochastic optimization: Algorithms and applications. Conference, Univ. of Florida, Tallahassee, FL, USA, February 20-22, 2000. Dordrecht: Kluwer Academic Publishers. Appl. Optim. 54, 223-264 (2001)., 2001. [ bib ] |
|
|
Carl Olsson, Anders P. Eriksson, and Fredrik Kahl. Solving large scale binary quadratic problems: Spectral methods vs. semidefinite programming. Computer Vision and Pattern Recognition, IEEE Computer Society Conference on, 0:1-8, 2007. [ bib | DOI ] |
|
|
M.B. Shchepakin. An orthogonal descent algorithm to find the zero of a convex function, unsolvability test, and rate of convergence. Cybern. Syst. Anal., 28(5):727-734, 1992. [ bib | DOI ] |
|
|
Ilse Fischer, Gerald Gruber, Franz Rendl, and Renata Sotirov. The Bundle Method in Combinatorial Optimization. Technical report, University of Klagenfurt, Austria., 2003. [ bib ] |
|
|
John E. Beasley. Lagrangian relaxation. John Wiley & Sons, Inc., New York, NY, USA, 1993. [ bib ] |
|
|
Antonio Frangioni. Generalized bundle methods. SIAM J. Optim., 13(1):117-156, 2002. [ bib | DOI ] |
|
|
Andrzej Cegielski. The Polyak subgradient projection method in matrix games. Discuss. Math., 13:155-166, 1993. [ bib ] |
|
|
B. T. Poljak. Minimization of Nonsmooth Functionals. USSR Computational Mathematics and Mathematical Physics, 9:14-29, 1969. [ bib ] |
|
|
|
Sprechstunde |
Raum |
Telefon |
|
|
|
n.V. |
MA 302 |
84185-210 |
groetschel |
|
|
|
n.V. |
ZIB |
84185-243 |
borndoerfer |
|
|
|
Markus Reuther |
n.V. |
ZIB |
84185-473 |
reuther |