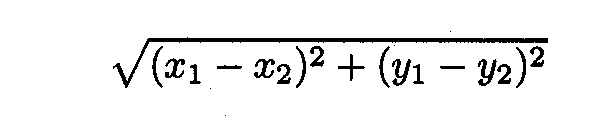
MATHEON
Konrad-Zuse-Zentrum für Informationstechnik BerlinIm Folgenden werden optimale Rundreisen für die drei verschiedenen Probleme (15, 25 und 40 Städte) vorgestellt. Es wurden präzise Koordinaten für die Lochmittelpunkte der Städte vorgegeben. Die Tische sind jedoch von einem Tischler manuell hergestellt worden, wodurch die Lochpositionen auf den Tischen ein wenig von den vorgegebenen Koordinaten abweichen. Es gibt sogar Abweichungen zwischen den beiden Spieltischen, die auch zu unterschiedlichen Längen der optimalen Rundreise führen. Die tatsächlich gebohrten Lochmittelpunkte wurden millimetergenau gemessen. Die für Spieltisch I (15 Städte vorgegeben) und Spieltisch II (25 Städte vorgegeben) gemessenen Koordinaten sind in Tabelle 1 und 2 zu finden. Die Entfernung zwischen zwei Orten mit Koordinaten (x1, y1) und (x2,y2) wird durch den euklidischen Abstand
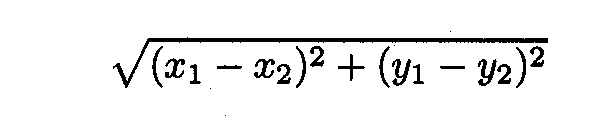
15-Städte-Problem (auf Spieltisch I)
Abbildung 1(a) zeigt die kürzeste Rundreise für das 15-Städte-Problem. Sie ist theoretisch 127,9 cm lang. Tatsächlich ist eine Schnurlänge von etwa 133 cm erforderlich. Es wurden außerdem die theoretisch zweit- und drittkürzeste Rundreise bestimmt. Vertauscht man die Besuchsreihenfolge der Städte Berlin und Potsdam, so erhält man die zweitkürzeste Rundreise. Ihre Länge ist 128,8 cm. Zur drittkürzesten Rundreise (ausgehend von der optimalen Rundreise) kommt man durch Vertauschen der Besuchsreihenfolge von Mainz und Saarbrücken. Diese Rundreise ist 129,9cm lang.
25-Städte-Problem (auf Spieltisch II)
Die optimale Rundreise für das 25-Städte-Problem ist in Abbildung 1(b) dargestellt. Sie ist theoretisch 175,9 cm lang. Die entsprechende Schnurlänge beträgt etwa 182 cm. Wenn man in dieser Rundreise Heidelberg zunächst auslässt, also nach Frankfurt direkt Würzburg besucht, und Heidelberg zwischen Freiburg und Trier einfügt, erhält man die zweitkürzeste Rundreise. Sie ist mit 176,0 cm nur geringfügig länger als die kürzeste. Ausgehend von der kürzesten Rundreise kommt man durch Vertauschen von Jena und Leipzig zur drittkürzesten Rundreise. Ihre Länge beträgt 177,0 cm.
40-Städte-Problem
Abbildung 1(c) zeigt eine kürzeste Rundreise für das 40-Städte-Problem. Diese optimale Rundreise ist jedoch auf den beiden Tischen unterschiedlich lang, auf Spieltisch I 206,9 cm und auf Spieltisch II 206,5 cm. In beiden Fällen beträgt die entsprechende Schnurlänge 216 cm.
Mehr zum Travelling-Salesman-Problem
Das Travelling-Salesman-Problem (TSP) ist das bekannteste und am intensivsten untersuchte Problem der kombinatorischen Optimierung. Einen umfassenden Überblick über das TSP, seine Geschichte, Lösungsalgorithmen und den gegenwärtigen Forschungsstand bietet das Buch
„The Traveling Salesman Problem: A Computational Study“ (Princeton University Press, 2007) von Applegate, Bixby, Chvatal und Cook.
„Die optimierte Odyssee“ (Grötschel und Padberg, 1999, deutsch)
„The Optimized Odyssey“ (Grötschel und Padberg, 2001, englisch)
„Schnelle Rundreisen: Das Travelling-Salesman-Problem“ (Grötschel 2007)
Eine umfangreiche Sammlung von konkreten Beispielen des Travelling-Salesman-Problems, die meisten stammen aus realen Anwendungen, z.B. der Leiterplattenproduktion oder des VLSI-Designs, ist in der TSPLIB zu finden. Diese enthält die Daten der Problembeispiele, die Länge der optimalen Lösungen sowie bildliche Darstellungen von Optimallösungen.
Kontaktpersonen:
Martin Grötschel und Andreas Tuchscherer
E-mail: {groetschel,tuchscherer}@zib.de
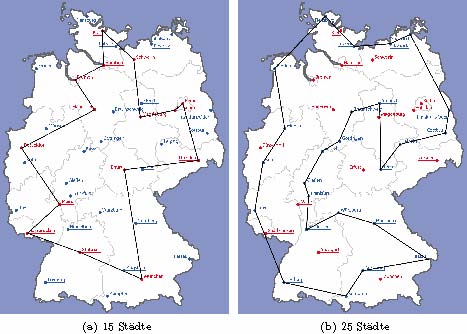
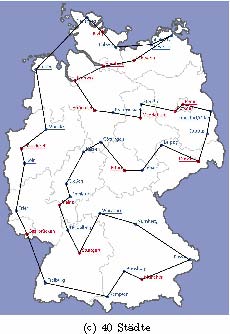
Abbildung 1: Optimale Rundreisen für die drei Probleme.
Stadt x-Koordinate y-Koordinate Bremen 144 158 Kiel 188 80 Hamburg 190 134 Schwerin 238 125 Düsseldorf 61 265 Hannover 175 205 Magdeburg 248 216 Berlin 315 195 Potsdam 303 205 Erfurt 222 300 Dresden 340 285 Saarbrücken 69 399 Mainz 120 354 Stuttgart 153 430 München 250 472 Flensburg 163 57 Emden 83 140 Lübeck 210 104 Stralsund 298 85 Rostock 266 100 Münster 100 235 Braunschweig 205 208 Stendal 249 194 Frankfurt/Oder 359 205 Köln 65 288 Kassel 158 270 Göttingen 186 254 Leipzig 281 259 Cottbus 353 242 Gießen 131 321 Jena 252 298 Frankfurt 137 340 Trier 52 363 Heidelberg 133 394 Würzburg 184 368 Nürnberg 240 384 Freiburg 98 477 Augsburg 222 458 Passau 325 441 Kempten 195 499 Tabelle1: Koordinaten der Städte auf Spieltisch I in Millimetern.
(Die vorgegebenen 15 Städte sind fettgedruckt.)
Der Nullpunkt liegt im Nordwesten und ist nicht eingezeichnet.
Stadt x-Koordinate y-Koordinate Bremen 144 157 Kiel 187 78 Hamburg 189 134 Schwerin 238 125 Düsseldorf 60 264 Hannover 175 204 Magdeburg 247 216 Berlin 315 194 Potsdam 303 205 Erfurt 222 299 Dresden 339 284 Saarbrücken 69 400 Mainz 120 354 Stuttgart 152 429 München 251 472 Flensburg 162 57 Emden 83 139 Lübeck 208 104 Stralsund 296 85 Rostock 265 100 Münster 99 234 Braunschweig 205 207 Stendal 249 194 Frankfurt/Oder 358 205 Köln 65 288 Kassel 158 270 Göttingen 185 254 Leipzig 281 259 Cottbus 352 241 Gießen 130 321 Jena 251 298 Frankfurt 137 341 Trier 52 363 Heidelberg 133 392 Würzburg 184 367 Nürnberg 240 383 Freiburg 97 477 Augsburg 222 458 Passau 326 439 Kempten 196 499
Tabelle 2: Koordinaten der Städte auf Spieltisch II in Millimetern
(Die vorgegebenen 25 Städte sind fett gedruckt.)
Der Nullpunkt (0,0) liegt im Nordwesten und ist nicht
eingezeichnet.