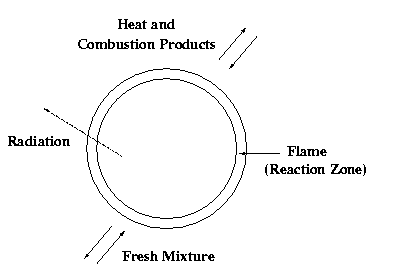
 |
|
combustion products (outwards) and of fresh mixture (inwards) together with radiative heat loss cause a zero mass-averaged velocity. |
| Responsible: | Jens Lang, Bodo Erdmann |
| Cooperation: | J. Fröhlich, University of Karlsruhe |
| Literature: |
J. Fröhlich, J. Lang, Two-dimensional Cascadic Finite Element
Computations of Combustion Problems, Comp. Meth. Appl. Mech. Engrg. 158
(1998), 255-267.
J. Lang, B. Erdmann, Adaptive Linearly Implicit Methods for Heat and Mass Transfer, Report ZR-00-21 (2000), Konrad-Zuse-Zentrum. |
Combustion problems are known to range among the most demanding for
spatial adaptivity when the thin flame front is to be resolved numerically.
This is often required as the inner structure of the flame determines global
properties such as the flame speed, the formation of cellular patterns
or even more important the mass fraction of reaction products (e.g. NOx
formation). A large part of numerical studies in this field is devoted
to the different instabilities of such flames. The observed phenomena include
cellular patterns, spiral waves, and transition to chaotic behaviour.
Laminar Flames through an Obstacle
Reaction Front in a Non-uniformly Packed Solid
Stability of Flame Balls: The profound understanding of premixed
gas flames near extinction or stability limits is important for the design
of efficient, clean-burning combustion engines and for the assessment of
fire and explosion hazards in oil refineries, mine shafts, etc. Surprisingly,
the near-limit behaviour of very simple flames is still not well-known.
Since these phenomena are influenced by bouyant convection, typically experiments
are performed in a micro-gravity environment. Under these conditions transport
mechanisms such as radiation and small Lewis number effects, the
ratio of thermal diffusivity to the mass diffusivity, come into the
play, see the next figure.
 |
|
combustion products (outwards) and of fresh mixture (inwards) together with radiative heat loss cause a zero mass-averaged velocity. |
Seemingly stable flame balls are one of the most exciting appearances
which were accidentally discovered in drop-tower experiments by Ronney
(1990) and confirmed later in parabolic aircraft flights. First theoretical
investigations on purely diffusion-controlled stationary spherical flames
were done by Zeldovich (1944). 40 years later his flame balls were predicted
to be unstable (1984). However, encouraged by the above new experimental
discoveries, Buckmaster and collaborators (1990) have shown that for low
Lewis numbers flame balls can be stabilized including radiant heat loss
which was not considered before.
 |
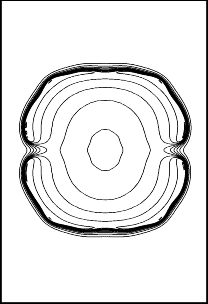 |
Two-dimensional flame ball with Le = 0.3, c = 0.01.
Iso-thermals T = 0.1, 0.2,..., 1.0 at times t = 10 and 30.
Typically, instabilities occur which result in a local quenching of
the flame as can be seen in the figure. After a while the flame is splitted
into two seperate smaller flames. Nevertheless, we found quasi-stationary
flame ball configurations, fixing the heat loss by radiation and varying
the initial radii for a circular flame.